Timing Attacks Demystified: From Theory to Real-World Key Recovery

Source: blog.zksecurity.xyz - Timing Attacks à la Kocher

Paul Kocher’s landmark 1996 paper revealed a critical vulnerability: cryptographic operations can leak secret key bits through their execution times. This type of side-channel attack exploits implementation details rather than the math behind the algorithms. Here’s a breakdown of how such an attack unfolds – from idealized models to real-world engineering challenges.

The Vulnerability: Conditional Multiplication in Modular Exponentiation

At the core of RSA and Diffie-Hellman is modular exponentiation. To speed this up, systems use the square-and-multiply method:

• Square at every bit
• Multiply only if the current exponent bit is 1

This conditional step leaks timing information: a “1” bit causes extra multiplication, making the operation slower.

def fast_exp(base, exponent, modulus):
    result = 1
    base = base % modulus
    while exponent > 0:
        if exponent & 1:  # extra multiply when secret bit = 1
            result = (result * base) % modulus
        base = (base * base) % modulus
        exponent >>= 1
    return result

Kocher’s insight was that by measuring many timings and applying statistical analysis, attackers can recover each bit of the secret exponent.

Part 1: Clean Models Yield Clear Results

Using a simplified instruction cost model that mimics modular multiplication along with “trial subtractions,” timing variations form a clear normal distribution. This happens because small, independent timing differences add up into a bell curve (Central Limit Theorem).

In this ideal setting, Kocher’s variance distinguisher compares the variance of timing residuals under different bit hypotheses. The hypothesis with lower variance is more likely correct, enabling perfect bit-by-bit key reconstruction.

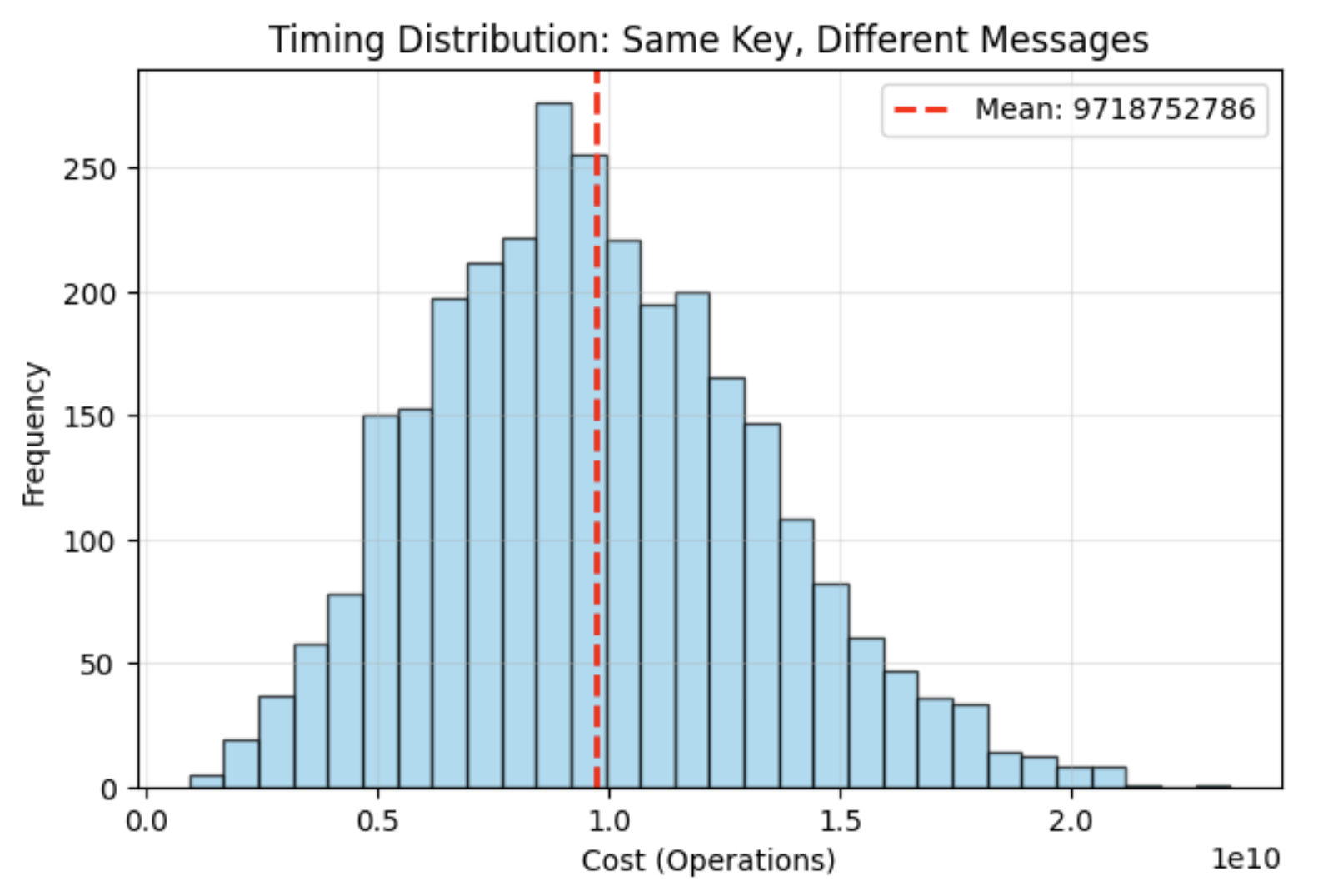
Example results from this model showed 100% accuracy recovering a 6-bit key from cost measurements.

Part 2: Real-World Noise Masks the Signal

With actual wall-clock timing on modern computers, noise sources abound:

• OS context switches and interrupts
• CPU frequency scaling
• Cache effects
• Python garbage collection

Measurements become noisy and variance differences nearly vanish, making it impossible to confidently identify correct bits-even after amplifying measurements 100x.

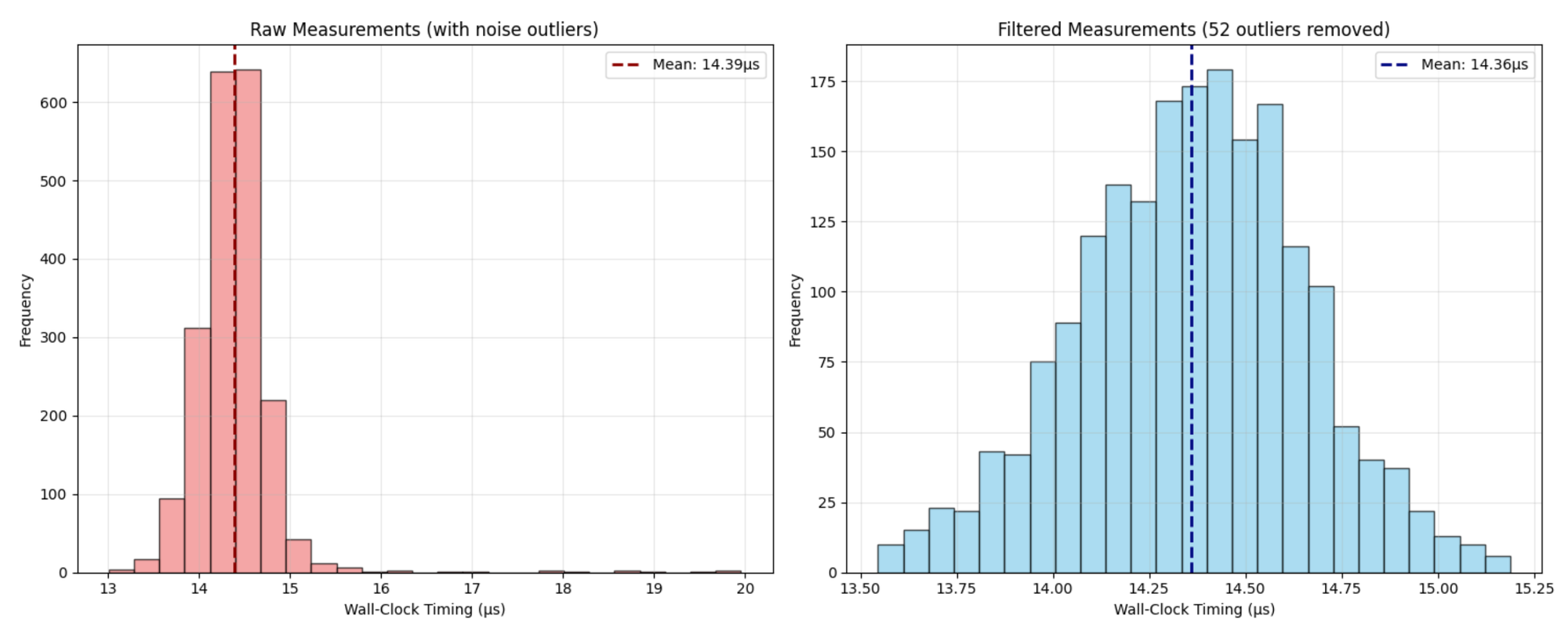
In practice, the attack only recovered 50% of bits correctly-equivalent to guessing.

Part 3: Engineering Practical Attacks

Overcoming noisy environments demands engineering hygiene and statistical tricks:

• Disable garbage collection during measurements
• Warm up CPU caches and branch predictors
• Alternate hypothesis testing order to reduce drift
• Use interquartile range (IQR) filtering for noise removal
• Bias selection toward messages with stronger timing differences

With these steps, a robust timing attack on a 12-bit exponent recovered bits with perfect accuracy on a 512-bit modulus, using far fewer messages and moderate amplification.

def iqr_filter(data, factor=1):
    # Filter outliers based on interquartile range (IQR)
    # Returns filtered data

Key Takeaways for Developers and Founders

• Timing attacks exploit subtle implementation details, not cryptographic math flaws.
• Real-world noise can severely hinder naive timing attacks-but well-crafted measurement and statistical engineering restore practicality.
• The best defense is using constant-time cryptographic implementations and side-channel-hardened libraries.

Don’t underestimate the attacker's engineering effort: vulnerabilities visible in theory often become exploitable with persistence and clever techniques.